Pour illustrer les différents concepts abordés, un exemple sera très utile. Supposons qu'à la suite d'une tempête, un marin naviguant en suivant la ligne de côtes, s'échoue sur des récifs. Le bateau étant bien équipé, il relève sa dernière position sur le GPS et monte dans le canot de sauvetage. Malheureusement, ce canot est dépourvu de rames. Les vagues et le vent l'emportent donc loin de son navire échoué. Définissons un référentiel de tel sorte que l'axe x soit parallèle à la côte et l'axe y lui soit perpendiculaire. La position du navire échoué dans ce référentiel est défini comme le point de référence de coordonnées (0,0). La position du canot de sauvetage est donc connu à l'instant \[ t_0=0 \]. Un peu plus tard, à l'instant t, le naufragé estime au jugé la distance qui le sépare de la côte. Le naufragé sait que son estimation est empreinte d'une erreur et il estime la variance de cette erreur \[s^o\]. Il se rappelle, par ailleurs, la position de l'épave et sait que le canot de sauvetage a dérivé malgré l'absence de courants marins prédominants dans cette région. Il suppose donc que la probabilité qu'il se trouve maintenant à la position \[(u^b,v^b)\] suit une loi normale de variance \[s^b\] qui dépend linéairement du temps écoulé. Après réflexion, il estime aussi que le processus de mesure au jugé n'est pas corrélé à celui de la dérive du canot. Il résume donc sa situation en faisant un schéma (Fig. 3).
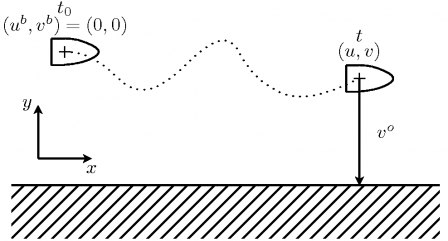
Fig. 3 : La géométrie de la situation du naufragé.